函数极限法则：揭示函数在极限处的行为规律与趋势，解析数学中的无穷世界

探索极限法则：解析数学中的无穷世界

在数学的世界中，极限是一个重要的概念，它揭示了函数在趋向某一特定点时的行为规律与趋势，通过对极限法则的研究，我们能够深入理解数学中的无穷世界，从而更好地把握函数的性质和行为。

极限法则的基本概念

极限法则是指当自变量趋近于某一特定值时，函数值趋近于某一确定的值，这个特定的值可以是有限数，也可以是无穷大，极限法则包括以下几个基本内容：

1、极限的定义：极限是描述函数在某一点附近的行为规律，它是一个精确的数学概念，用以研究函数在某一区间内或某一特定点附近的性质。

2、极限的性质：极限具有唯一性、局部性、保号性等性质，这些性质为极限的研究提供了理论基础。

3、极限的计算：极限的计算方法包括直接计算、洛必达法则、夹逼定理等，这些方法为求解极限问题提供了有效的手段。

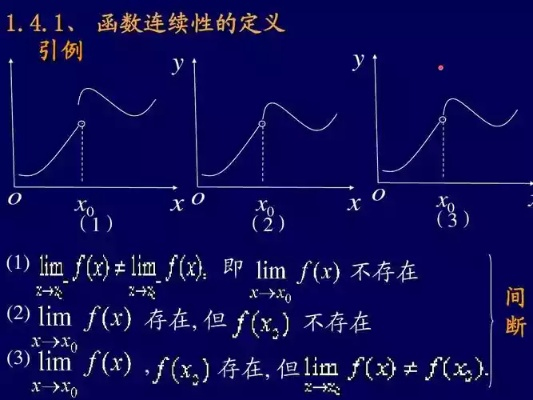
极限法则在数学中的应用

1、极限与导数的关系：极限是导数的基础，导数是极限的推广，通过极限法则，我们可以求出函数在某一点处的导数，从而研究函数的增减性、凹凸性等性质。

2、极限与积分的关系：积分是极限的推广，通过极限法则，我们可以求解定积分，从而研究函数在某一区间内的累积变化。

3、极限与级数的关系：级数是极限的推广，通过极限法则，我们可以研究级数的收敛性与发散性，从而求解级数的和。

常见问题解答（FAQ）

1、问：为什么极限在数学中如此重要？

答：极限是研究函数性质的重要工具，它可以帮助我们理解函数在某一区间内或某一特定点附近的行为规律，极限法则为数学分析提供了基础，使得我们可以求解导数、积分等数学问题。

2、问：如何求解极限问题？

答：求解极限问题需要掌握极限的基本概念和计算方法，常见的极限计算方法包括直接计算、洛必达法则、夹逼定理等，在实际求解过程中，需要根据具体问题选择合适的方法。

3、问：极限与无穷大有何关系？

答：无穷大是极限的一种特殊情况，当自变量趋近于无穷大时，函数值也趋近于无穷大，极限法则可以用来研究无穷大附近的函数行为。

参考文献

1、华东师范大学数学系《数学分析》编写组. 数学分析（上册）[M]. 北京：高等教育出版社，2003.

2、张筑生. 数学分析原理[M]. 北京：科学出版社，2007.

3、严士健，谢力，赵进义. 数学分析[M]. 北京：高等教育出版社，2011.

通过对极限法则的研究，我们能够深入理解数学中的无穷世界，探索函数在极限处的行为规律与趋势，极限法则不仅在数学领域具有重要意义，还在物理学、工程学等领域发挥着重要作用，掌握极限法则，有助于我们更好地理解和应用数学知识，解决实际问题。